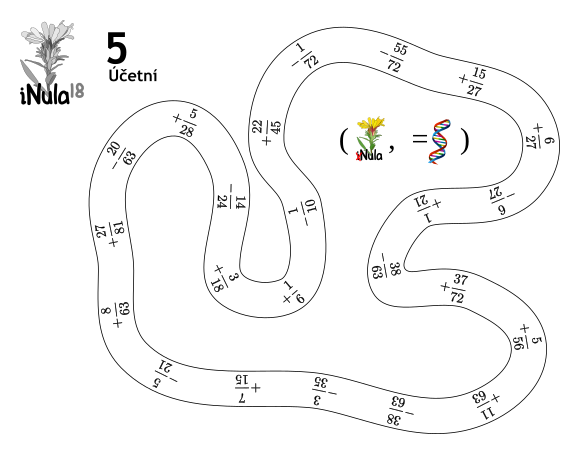
Šifra číslo 5, Lesní lom
Autor šifry: Yeti
Nápověda
|{1/9, 1/8, 1/7, 1/6, 1/5, 2/9, …, 7/8, 8/9}| = 27
Řešení
Divný okruh obsahuje kladné a záporné zlomky, Uvnitř jsou jakési závorky a obrázky. Vnitřek inrerpretujeme jako (NULA, JE-DNA), tedy otevřený interval (0,1). Šifra bude zřejmě matematická a budeme se muset i na zlomky podívat matematicky.
Čitatelé jsou celkem divočina, zato ve jmenovatelích rychle odhalíme systém. Jsou to vždy součiny dvou čísel 2–9 a dva sousední zlomky mají vždy společný faktor. Jsou zjevně schválně nevykrácené, abychom to snáz zjistili. Faktory jmenovatelů tedy tvoří cyklickou sekvenci, kterou si můžeme i napsat do prázdných míst mezi zlomky. Která jsou ostatně podezřele velká, takže něco tam vepsat určitě patří.
Matematik v týmu nyní poznamená, že kdyby vepsaná čísla (získaná ze jmenovatelů) byla také jmenovatelé zlomků, tak by akorát sedělo, že by zlomky v zadání byly jejich rozdíly. To dává přirozeně řadu zlomků, kde vždy dva po sobě mají společný faktor ve jmenovateli. A chceme raději rozdíly. Jednak kvůli znaménkům a jednak kvůli kruhu. (A pokud si někdo dal práci a všechno sečetl, zjistil, že součet je nula, což teorii potvrzuje.)
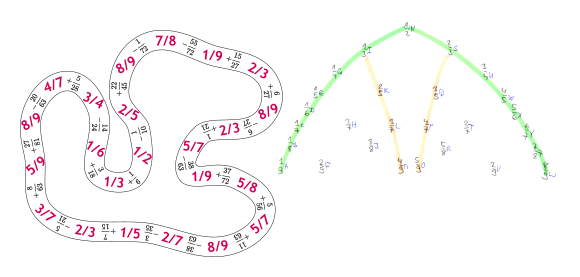
K čemu máme informaci (0,1)? Zlomky, které hledáme, budou zřejmě z tohoto intervalu. Teď se potřebujeme někde chytit. To jde naštěstí snadno. Jmenovatele zlomků známe, takže máme pro rozdíly víceméně vždy jen dvě symetrické možnosti typu 1/7 − 1/8 a 7/8 − 6/7. Zda se pohybujeme v oblasti velkých nebo malých čísel, odhadneme z koncentrace znamének okolo. Ještě chytřejší je všimnout si poloviny, která může být jen 1/2, a tudíž je jednoznačná. Pak už to jde snadno a dostaneme sekvenci zlomků, od nejvyššího bodu 7/8, 1/9, 2/3, 8/9, 2/3, 5/7, 1/9, 5/8, 5/7, 8/9, 2/7, 1/5, 2/3, 3/7, 5/9, 8/9, 4/7, 3/4, 1/6, 1/3, 1/2, 2/5, 8/9.
To by mohla být tajenka, když dokážeme na zlomky namapovat abecedu. Všech zlomků se jmenovatelem 2–9 (nezkrácených) je v intervalu 36. Jenže nejsme na ročníku s iNulí 36-abecedou a raději bychom normálnější počet. Můžeme si všimnout, že nové zlomky jsou všechny v základním tvaru. To je podeželé, protože nezkrácených je dost na to, aby tam nějaké byly, pokud se používají. Kolik je tedy různých zlomků neboli zlomků v základním tvaru? Těch je 27. Vzpomeneme si na radu, že když máme něčeho 27, máme nechat poslední znak prázdný a namapujeme abecedu podle velikosti s 8/9 jako prázdným znakem na konci.
Zlomky se dají seřadit s použitím výpočetní techniky, ale není to zapotřebí. Jednak jsou symetrické kolem 1/2 a jednak se v každé polovině všechny až na tři seřadí triviálně (podél barevných oblouků na obrázku). Zbylé tři už není problém zatřídit.
Tím dostaneme tajenku (včetně mezer) ZAS_START_HESLO_PUDINK_. Jdeme tedy zpátky do rokle.
Nálepkovník
Tým: Přizdi
Čas: 20:03
N/Z: 0/0
Tým: Zakysnutí hrošíci
Čas: 20:20
N/Z: 1/0
Tým: Do lesíčka na sekanou
Čas: 20:47
N/Z: 1/0
Tým: Buridanův osel
Čas: 20:47
N/Z: 1/1
Tým: Mostíci
Čas: 20:49
N/Z: 1/0
Tým: iTým
Čas: 20:52
N/Z: 0/0
Tým: Žádný hroty!
Čas: 20:57
N/Z: 1/1
Tým: Katastrof technik
Čas: 21:03
N/Z: 1/1
Tým: Nejostřejší tužky v penálu
Čas: 21:04
N/Z: 1/1
Tým: voy-a-ger
Čas: 21:14
N/Z: 1/1
Tým: TSUNAVLNAMI
Čas: 21:24
N/Z: 2/1
Tým: LEGOutschen turisten
Čas: 21:40
N/Z: 3/2
Tým: SULTÁNISTÁN
Čas: 22:01
N/Z: 3/0
Tým: Qapem Qítězství
Čas: 22:13
N/Z: 1/0
Tým: Just Karel
Čas: 22:15
N/Z: 3/2
Tým: Quo Vadis
Čas: 22:17
N/Z: 4/3
Tým: žufouni
Čas: 22:22
N/Z: 3/2
Tým: Letní Me2di
Čas: 22:23
N/Z: 3/1
Tým: MurmaŇi
Čas: 22:24
N/Z: 3/2
Tým: Morek Dvorek
Čas: 22:24
N/Z: 4/2
Tým: Potkali se tři
Čas: 22:24
N/Z: 3/1
Tým: Antropoid
Čas: 22:26
N/Z: 3/1
Tým: Pralinky zvlášť
Čas: 22:31
N/Z: 2/0
Tým: Ptáci na tahu
Čas: 22:51
N/Z: 4/2
Diskuse
- 7. října 2025 v 09:51
Yeti, to je třeba věc, která nás celou dobu nenapadla. Naše odpověď byla "protože to tak orgové chtěli". Vlastně jsme to jen nějak dobili po nápovědě, protože jsme se zahrabali do důsledků principu (např. to, že zlomky nejsou v základním stavu ulehčuje dedukci jmenovatelů, ale vede k otázce, proč to není vykráceno, na kterou může být odpověď třeba taková, že ve skutečnosti nejde tolik o čísla, ale o číslice...).
- 7. října 2025 v 09:11
Dark: Když zjistím, že je součet na uzavřené smyčce nula, vím, že ta čísla vznikla jako rozdíly nějakého jiného popsání smyčky čísly. Je to primární informace, kterou jsem z toho dostal a nemůže to být náhoda. Zkouším proto rekonstruovat to původní popsání – obzvlášť když mi šifra nabízí pěkně mezery, kam bych měl psát ta původní čísla. Šifra se dá řešit bez pozorování o nulovém součtu, ale s ním už bych neměl nikam uhnout. Co jste z toho jiného těžili?
- 7. října 2025 v 09:09
@Dark: Náš postup spočíval v rozložení jmenovatelů na násobek dvou blízkých čísel, pak najití domino vlatnosti. Rozhodnutí, že mezi již ukázané zlomky chceme napsat zlomky, které budou mít ve jmenovateli odpovídající číslo (to které mají jeho sousedi společné). Začli jsme u x/9 +37/72 = y/8. Z toho tuším vyšlo x=1 a y=5. A na druhý pokus už jsme zvládli takhle udělat celý cyklus. Pak jsme si všimli, že jmenovatel je z <2, 9> a čitatel <1, 8> a po zavrhnutí semaforu nezbylo než si spočítat počty a s nalezenou 27 to dodělat.
Přijde mi, že u iNulých těžkých šifer to často bývá tak, že dokud se držíš orgovského postupu, tak všechno krásně sedí a dává smysl. Jak jednou ustoupíš a/nebo si všimneš něčeho neúmyslného, tak už se těžko dostává na správnou stopu.
- 6. října 2025 v 20:57
Taky druhý zákys po startu. My jsme se zasekli na pozorování, že různé intervaly na trase dosahují součtu nula, a z toho se dá těžit spousta informací. Nápověda pomohla, ačkoli jsme se nezbavili pachuti s myšlenkou, jak se na to mělo bez nápovědy přijít?
- 5. října 2025 v 21:01
Tady přišla druhá krize po té první na startu. Slovní hříčku jsme prolomili rychle, společné faktory jsme taky objevili, ale pořádně jsme nevěděli, co s nimi. Tak jsme na to šli tou složitější cestou: začali jsme někde od nuly a poustupně dopočítávali zlomky po cestě. Ž je to "tak trochu" správně jsme si potvrdili tím, že jsme došli opět k nule, ale tušili jsme, že to není "úplně" správně, protože jsme měli v dopočítaných hodnotách nulu a ta to intervalu nepatřila. Jenže o kolik to zvednout a proč zrovna o tolik? Na to jsme nedokázali až do nápovědy přijít.
Šifra rozhodně zajímavá.
- 5. října 2025 v 17:03
Pro nás vrchol hry a náš nejlepší výkon. Minimálně relativně vůči zbytku pole. Všechno zapadlo, každý přidal kousek a šifra náš vedla přesně k řešení.
- 5. října 2025 v 16:18
Tady jsme konečně zvládli naplno využít vzdáleně hrajícího Kubu, který to celé řešil v Excelu. Prakticky hned jsme tedy věděli, že součet zlomků je 0 a že rozsah kumulovaných hodnot je 7/9. Následně jsem si všiml, že čísla ve jmenovatelích jsou součiny 2 až 9 a že fungují jako domino. Michal zas pochopil rébus (0,1). V tuhle chvíli jsme mohli mít vyluštěno, ale místo toho jsme se z nějakého důvodu rozhodli to celé řešit jako soustavu diofantických rovnic, ze které nám vypadla spousta řešení – ta, co vzniknou přičtením celého čísla <i>k</i> ke každému ze zlomků. Takže jsme po 3 hodinách vzali nápovědu a plácli se do čela. Emoce: stud.